Statistische Signifikanz

Was ist statistische Signifikanz?

Die statistische Signifikanz ist ein Maß dafür, wie ungewöhnlich die Ergebnisse Ihres Experiments wären, wenn es tatsächlich keinen Unterschied in der Leistung zwischen Ihrer Variation und der Basislinie gäbe und die Diskrepanz im Auftrieb allein auf den Zufall zurückzuführen wäre.

Für Online-Unternehmen, Vermarkter und Werbetreibende, die A/B-Tests durchführen (wie z.B. das Testen von Conversion Rates, Anzeigentexten oder E-Mail-Betreffzeilen), wird dies immer wichtiger.

Das Erreichen einer statistischen Signifikanz trägt dazu bei, dass die aus Experimenten gezogenen Schlussfolgerungen zuverlässig sind und nicht auf zufälligen Schwankungen der Daten beruhen.

Den meisten Experimenten gelingt es jedoch nicht, ein erhebliches Signifikanzniveau zu erreichen. Hier ist der Grund dafür:

• Die Änderungen sind zu gering: Die meisten Änderungen an den Erlebnissen der Besucher sind nicht aussagekräftig und erreichen aufgrund von Stichprobenfehlern keine Signifikanz.
• Niedrige Conversion Raten: Die meisten Datensätze verwenden Metriken mit einem niedrigen Ausgangswert, was oft zu Testergebnissen mit erheblichen Standardabweichungen führt.
• Zu viele Ziele: Oft konzentrieren sich die Teams nicht auf die entscheidenden Metriken, die mit ihrer Hypothese übereinstimmen. Dies führt dazu, dass die Forschungsergebnisse die Signifikanzschwelle nicht erreichen.

Warum ist das Konzept der statistischen Signifikanz so wichtig?

Die statistische Signifikanz hilft Unternehmen, fundierte Entscheidungen auf der Grundlage von Daten und nicht von zufälligen Schwankungen zu treffen. Sie hängt von zwei Schlüsselfaktoren ab:

1. Die Stichprobengröße: Die Anzahl der Teilnehmer an Ihrem Experiment. Größere Stichproben liefern im Allgemeinen zuverlässigere Ergebnisse. Bei Website-Tests bedeutet mehr Verkehr schnellere und genauere Ergebnisse.
2. Effektgröße: Das Ausmaß des Unterschieds zwischen Ihren Testvarianten. Sie zeigt an, wie stark sich Ihre Änderungen ausgewirkt haben.

Zufallsstichproben sind entscheidend, um den statistisch signifikanten Unterschied zu überbrücken und genaue Ergebnisse zu erhalten. Wenn Sie Ihre Testvariationen nicht nach dem Zufallsprinzip auf Ihre Zielgruppe verteilen, kann es zu Verzerrungen kommen. Ein Beispiel: Wenn alle Männer Version A und alle Frauen Version B sehen, können Sie die Ergebnisse nicht fair vergleichen, selbst bei einer 50:50-Aufteilung. Die Unterschiede im Verhalten könnten auf das Geschlecht zurückzuführen sein, nicht auf Ihre Testvarianten.

Ein Beispiel für die Auswirkungen in der Praxis: In Branchen wie der Pharmaindustrie kann die statistische Signifikanz in klinischen Studien über die Wirksamkeit eines Medikaments entscheiden. Dies kann die Finanzierung durch Investoren und den Erfolg oder Misserfolg eines Produkts beeinflussen.

Insgesamt hilft Ihnen die statistische Signifikanz dabei, zwischen echten Verbesserungen und Zufällen zu unterscheiden und so bessere Geschäftsentscheidungen zu treffen.

Testen Ihrer Hypothese

Die statistische Signifikanz wird in der Praxis vor allem beim Testen von Hypothesen verwendet. Sie möchten zum Beispiel wissen, ob die Änderung der Farbe einer Schaltfläche auf Ihrer Website von rot zu grün dazu führt, dass mehr Menschen darauf klicken. Wenn Ihre Schaltfläche derzeit rot ist, nennt man das Ihre "Nullhypothese", die die Form Ihrer Experiment-Basislinie annimmt. Wenn Sie Ihre Schaltfläche grün färben, wird dies als "Alternativhypothese" bezeichnet.

Um den beobachteten Unterschied in einem statistischen Signifikanztest zu bestimmen, sollten Sie auf zwei Ergebnisse achten: den p-Wert und das Konfidenzintervall.

1. P-Wert: Der P-Wert ist die Wahrscheinlichkeit, dass die Beweise für einen Leistungsunterschied zwischen Ihrer Variante und der Ausgangshypothese gleich stark oder stärker ausfallen. Dabei wird davon ausgegangen, dass es tatsächlich keinen Unterschied zwischen den beiden gibt und jeder beobachtete Anstieg ausschließlich dem Zufall geschuldet ist.
2. Konfidenzintervall: Das Konfidenzintervall ist ein geschätzter Wertebereich, der wahrscheinlich, aber nicht garantiert, den unbekannten, aber exakten Wert enthält, der Ihre Zielpopulation zusammenfasst, wenn ein Experiment mehrmals wiederholt wurde.

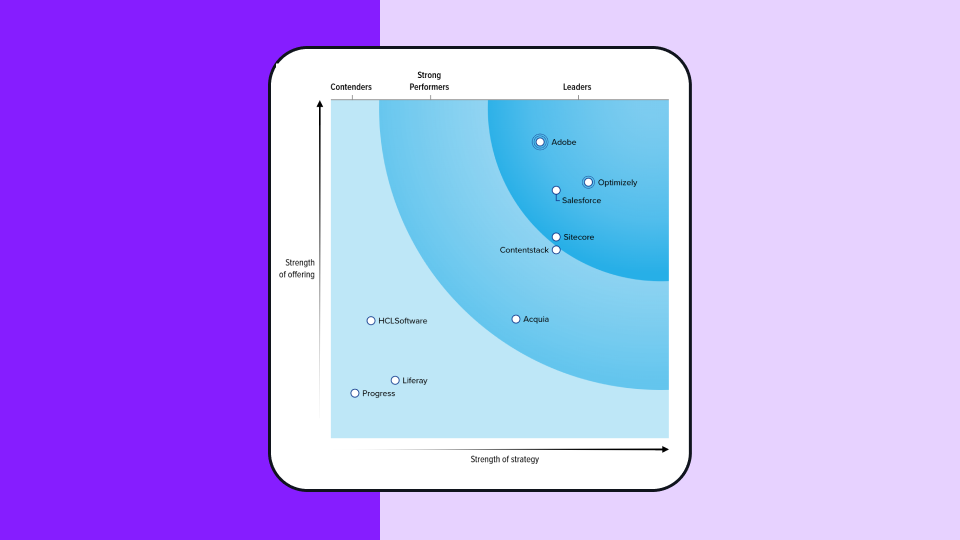
Erhalten Sie mit Stats Engine immer gültige Ergebnisse

Um gültige Ergebnisse aus Experimenten zu erhalten, die mit klassischer Statistik durchgeführt werden, sind strenge Richtlinien erforderlich: Legen Sie im Voraus einen minimalen nachweisbaren Effekt und eine Stichprobengröße fest, schauen Sie sich die Ergebnisse nicht an und testen Sie nicht zu viele Ziele oder Variationen gleichzeitig. Diese Richtlinien können mühsam sein und, wenn sie nicht sorgfältig befolgt werden, zu stark verzerrten und zweifelhaften Testergebnissen für Statistiker führen.

Glücklicherweise können Sie die praktische Signifikanz Ihrer Experimente mit Stats Engine, dem in Optimizely integrierten fortschrittlichen Statistikmodell, leicht ermitteln. So berechnen Sie die geschätzte Dauer Ihres Experiments:

• Benötigte Gesamtbesucherzahl = Stichprobengröße × Anzahl der Variationen
• Geschätzte Laufzeit = Benötigte Gesamtbesucherzahl ÷ Durchschnittliche tägliche Besucherzahl

Stats Engine arbeitet mit einer Kombination aus sequentiellen Tests und der Kontrolle der Falschentdeckungsrate, um Ihnen schneller zuverlässige Ergebnisse zu liefern, unabhängig von der Stichprobengröße und der Art der Daten. Dieser Ansatz wird in Echtzeit aktualisiert und ermöglicht Folgendes

• Überwachung der Ergebnisse in Echtzeit
• Adaptives Testen, das sich an die tatsächliche Effektgröße anpasst
• Schnellere Entscheidungsfindung ohne Beeinträchtigung der Datenintegrität

Mit Stats Engine sollte die statistische Signifikanz im Allgemeinen im Laufe der Zeit zunehmen, wenn mehr Beweise gesammelt werden. Diese Beweise gibt es in zwei Formen:

• Größere Unterschiede in der Conversion Rate
• Unterschiede in der Conversion Rate, die auch bei mehr Besuchern bestehen bleiben

Sehen Sie sich den vollständigen Stats Engine Bericht an.

Erfolgsmethoden für das Erreichen statistischer Signifikanz

Wenn Sie statistische Tests durchführen, kann es schwierig sein, eine statistische Signifikanz zu erreichen. Hier sind einige Erfolgsmethoden, die Sie befolgen können:

• Führen Sie Tests für mindestens einen Geschäftszyklus (7 Tage) durch
• Wählen Sie primäre und sekundäre Metriken sorgfältig aus
• Entwerfen Sie Experimente, die einen signifikanten Einfluss auf das Nutzerverhalten haben können.